Spare parts obsolescence and redundancy are an important factor in managing the lifecycle of a typical high value system.
Electronic components typically have short production lifecycles, typically 2-5 years and even military suppliers have difficulty maintaining production past this point without special government funding. Here is a question that was recently asked by one of our customers:
1) I have an item that will not be repaired nor is there a possibility the item can get resupplied from the vendor, nor will it get tested for faults, so I believe the No Fault Find Ratio and repair turnaround time is not relevant in my situation.
2) When the item fails a new item will be issued from stores and the failed item will not get tested nor will the item get replaced. I need to find out what the ideal sparing is based on no testing, no resupply and no repair for item.
3) Adjusting the No Fault Find Ratio and Repair Turn Around Times adjusts my recommended spares level, what should I put into the model to indicate a no testing, no resupply, no repair inventory management policy?
Problem Analysis
The client is describing what is known as a “discard on failure repair policy” and because there will no chance of resupply from the supplier the client will need to forecast the requirements for what is known as a “lifetime buy”.
Light bulbs are examples of items that have a discard on failure repair policy.
The client assumes that the “No Fault Found Ratio” is irrelevant. This is incorrect. Items will still be removed in error. Testing might not be conducted but the NFF ratio will still be present. In real-life maintenance, people remove LRUs and either discard them or send them back for repair when there isn’t anything wrong with them.
I recently watched a maintenance engineer repair a central heating boiler under warranty and he must have removed and discarded at least four items before he fixed the fault.
What should you do if you do not know the NFF Ratio?
In this case the Project Manager should liaise with maintenance specialists and subject matter experts to try to establish a reasonable figure. A technique called “Qualification by Similarity” can be adopted where other similar installations are reviewed and reasonable figures deduced. Once a figure has been established it should be recorded somewhere in the project documentation. Often logistic specialists will approximate by guessing a figure without consulting subject matter specialists. This is obviously to be discouraged.
The client also assumes that the “Repair-Turn-Around-Time” is irrelevant. This is also incorrect. In this case it would be better to think of a “Replenishment Delay” rather than a Repair-Turn-Around-Time.
Nearly all spare parts forecasting solutions use the Poisson Distribution to forecast the likelihood of a certain number of events occurring when something else is expected.
In this situation we are trying to establish the likelihood that we will run out of spare parts during the life of the equipment.
The Replenishment Delay in a Lifetime Buy situation is the whole life of the equipment. For example, if the system will have an operational life of 20-years then the Repair-Turn-Around-Time becomes 20-years.
Sample Calculation
Consider the following example. An aircraft Flight Management System has a special memory chip that is going out of production. The aircraft is expected to operate for a further 20-years and the operator needs to perform a Lifetime Buy. How many parts should the operator order?
Logistic Data
Equipment: ABC Memory Chip
Aircraft in Service: 146
LRUs Per Aircraft: 6
Chips Per LRU: 12
Daily Operating Hours: 18 hours/day
Mean Time Between Failure: 600,000 hours
No Fault Found Ratio: 20%
Expected Life: 20 years
Unit Cost: $146
MTBSO Goal: > 1000 Years
Step 1: Calculate the Units System
[6 LRUs Per Aircraft] x [12 Chips Per LRU] = 72
Step 2: Refactor the Expected Life into a pseudo Repair-Turn-Around-Time
[20 years] x [365.25 days/year] = 7305 days expected lifetime
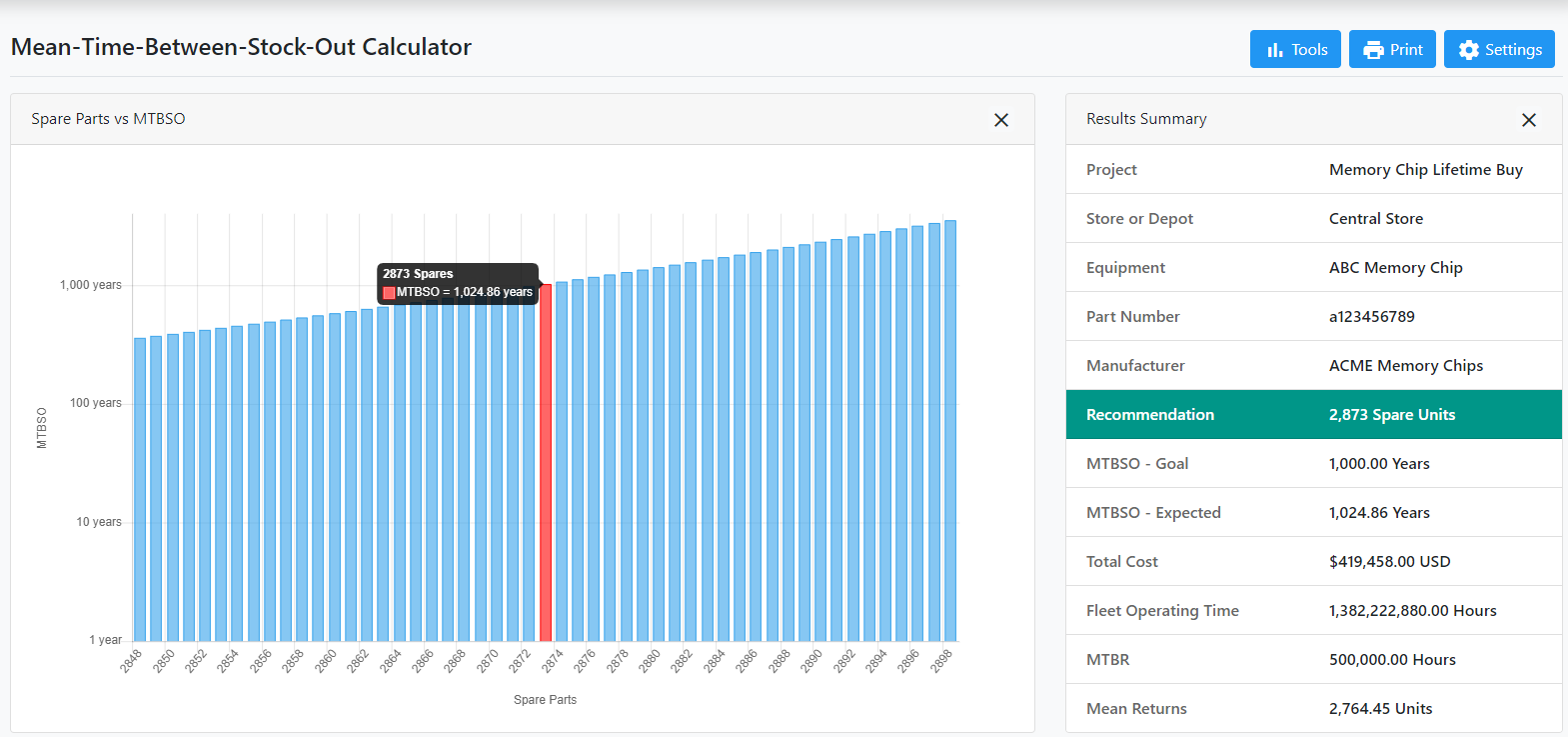
Step 3: Model the data in Spares Calculator
By entering that data in the into Spares Calculator you can see that we would need to procure 2,873 memory chips at a total cost of $419,458.00 to meet a MTBSO (Mean Time Between Stock-Out) goal of greater than 1000 years.